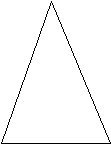
A
           1) Using a ruler measure AB and AC. What do you notice?
            This is an example of an       triangle.
     
           2) Measure angle ABC and ACB. What do you notice?
            Therefore, if a triangle has congruent sides, the angles
            opposite must be      .  
     
    B       C
     
     
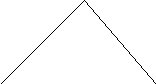      D      3) Measure angle D    . Measure angle E    
            Measure angle DFG.
     
           4) Make a conclusion regarding the relationship between
               angles D and E and F.
    E       F    G                
     
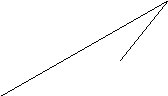          H  5) Measure sides HI, HJ, and IJ.
     
           6) Measure angles H, I and J.

        J    7) What type of triangle is HIJ?
     
    I        8) If a triangle has sides that are unequal then the angles are
                 .
     
     
     
    In triangle ABC below, label the following:
    a) Vertex  b) Sides  c) 1 interior angle  d) exterior angle  e) altitude
    e) median
     
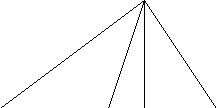          B                
     
     
     
     
    A

        E D C       F
     
     
     
    Fill in: The sum of any two sides of a triangle must be       the 3rd side.
    Examples:
     
    1)  Find the measure of angle FGH.
    F
                       
     
    H           E
          G
     
    2)  If the ratio of the degree measures of a triangle are 1: 3: 5, what is the degree of the measure of the smallest angle?
     
     
     
     
    3) LMN and LNO below are isosceles triangles with the measure of angle MLN = 55 and the measure of angle LON equal to 60. If LN = LM and LN = NO, what is the measure of angle MNO?
     
        M
     
     
     
      N      L
     
     
     
     
     
          O

    Back to top